Modeling of Post-Myocardial Infarction: ODE/PDE Analysis with R presents mathematical models for the dynamics of a post-myocardial (post-MI), aka, a heart attack. The mathematical models discussed consist of six ordinary differential equations (ODEs) with dependent variables Mun; M1; M2; IL10; Tα; IL1. The system variables are explained as follows: dependent variable Mun = cell density of unactivated macrophage; dependent variable M1 = cell density of M1 macrophage; dependent variable M2 = cell density of M2 macrophage; dependent variable IL10 = concentration of IL10, (interleuken-10); dependent variable Tα = concentration of TNF-α (tumor necrosis factor-α); dependent variable IL1 = concentration of IL1 (interleuken-1).
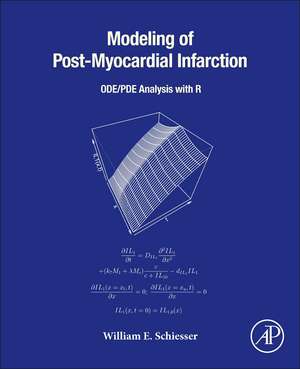
The system of six ODEs does not include a spatial aspect of an MI in the cardiac tissue. Therefore, the ODE model is extended to include a spatial effect by the addition of diffusion terms. The resulting system of six diffusion PDEs, with x (space) and t (time) as independent variables, is integrated (solved) by the numerical method of lines (MOL), a general numerical algorithm for PDEs.

• Includes PDE routines based on the method of lines (MOL) for computer-based implementation of PDE models
• Offers transportable computer source codes for readers in R, with line-by-line code descriptions as it relates to the mathematical model and algorithms
• Authored by a leading researcher and educator in PDE models